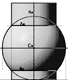
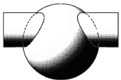
| Tra un cilindro e una sfera.
|
 |
 |
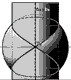 |
 |
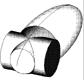
| Tra un cilindro ed una ellissoide.
|
 |
|||

Poniamo il caso (fig. 5) di due superfici con gli assi a, b incidenti ed appartenenti ad un piano di profilo. La quartica d’intersezione è digrammica e simmetrica rispetto a due piani: uno è g, l’altro è b, passante per C e con giacitura perpendicolare all’asse b, del toro.
Per la determinazione della quartica formata in questo caso dai punti comuni ai paralleli del toro ed a quelli della superficie ad asse verticale, ci serviamo di sfere ausiliarie secanti ambedue le superfici. Le dette sfere hanno il centro nel punto d’incontro C tra gli assi, quindi si ripresenta il caso d’intersezione tra superfici con assi coincidenti (perché l'asse del toro coincide con uno degli infiniti assi della sfera).cioè permesso, si deduce che le intersezioni tra le sfere ausiliarie e le superfici sono circonferenze. Nel caso in esame l’intersezione tra le sfere ausiliarie con il toro, sono circonferenze che appartengono ai piani frontali e perciò hanno la 2° proiezione in vera forma. In 1°P.O. si presentano come segmenti (proiezioni dei diametri).
Nel caso d’intersezione tra le dette sfere con la superficie ad asse verticale, le ciconferenze-sezioni appartengono a piani orizzontali e perciò hanno la 1°P.O. in vera forma, e la 2°P.O. come segmenti.
I punti della quartica sono dunque individuabili sia in 1°che in 2°P.O. come punti comuni alle sezioni prodotte da ogni singola sfera ausiliaria con le due superfici.
Ad esempio il punto E, appartiene sia al parallelo Q del toro, che al parallelo e, sezioni , rispettivamente, della sfera con il toro e con la superficie principale. Il raggio di questa sfera secante è il segmento C?D, poiché D appartiene allo stesso parallelo-secante Q relativo al toro.
L’individuazione dei punti, A, B, di massima e di minima quota della quartica (riferendosi solo al ramo destro) è immediata e non richiede l’ausilio di sfere secanti , poiché detti punti appartengono al piano frontale b (piano di simmetria longitudinale) e quindi la 2° P.O. delle sezioni coincide con la seconda proiezione dei contorni apparenti di entrambe le superfici, rispettivamente, i paralleli, D, F, di raggio massimo e minimo del toro e la generatrice H della superficie ad asse verticale .
--------------------------------
Intersezione di due superfici, di cui una a generatrice rettilinea e l'altra a generatrice curva.
Intersezione tra un cilindro e una sferaNei vari casi il tipo di curva d’intersezione dipende sia dalla reciproca posizione degli assi delle due superfici che dalla misura del loro diametro. I casi sono i seguenti:

Punti notevoli della quartica d'intersezione nella rappresentazione in P.O. :
la 1° P.O. della circonferenza, g1 ha il
diametro individuabile in 2°P.O come segmento delimitato dai punti d’incidenza tra t"a e il contorno apparente della sfera.
La 1°P.O. delle generatrici, b1, d1 coincide con la 1° P.O. delle generatrici di contorno apparente del cilindro. La 2° P.O. b2,d2 coincide con la seconda traccia del piano a(piano proiettante in 2° proiezione).
La 1°P.O. della circonferenza, f 1 coincide con t'b (piano proiettante in prima proiezione).
La 2°P.O. f 2, ha diametro individuabile in 1°P.O come segmento delimitato dai punti d’incidenza tra t"a e il contorno apparente della sfera.
La 1° P.O. delle generatrici, h1, i1 coincide con prima traccia del piano, t'b. la 2° P.O., h2, i2 coincide con la 2° P.O. delle generatrici di contorno apparente del cilindro.