 in cui il cilindro è posizionato in
modo tale da avere due generatrici, e e f, tangenti alla sfera, il risultato dell'intersezione è un quartica costituita da un solo ramo detta monogrammica.
in cui il cilindro è posizionato in
modo tale da avere due generatrici, e e f, tangenti alla sfera, il risultato dell'intersezione è un quartica costituita da un solo ramo detta monogrammica.Si pone il caso (fig.7)  in cui il cilindro è posizionato in
modo tale da avere due generatrici, e e f, tangenti alla sfera, il risultato dell'intersezione è un quartica costituita da un solo ramo detta monogrammica.
in cui il cilindro è posizionato in
modo tale da avere due generatrici, e e f, tangenti alla sfera, il risultato dell'intersezione è un quartica costituita da un solo ramo detta monogrammica.
Per trovare alcuni dei punti notevoli della quartica, come e, f quelli in cui la quartica è tangente le generatrici del cilindro. A tale fine si considera il piano a che passa per il centro della sfera ed ha giacitura perpendicolare all’asse del cilindro (il piano di simmetria trasversale della quartica). le sezione del piano a con la sfera e con il cilindro sono, rispettivamente, le circonferenze Q e d F. I punti in comuni a tali circonferenze sono quelli cercati G, F.
Altri punti notevoli sono A ed B: quelli di minima e di massima quota della quartica, la cui determinazione è immediata e avviene assumendo il piano frontale b, che contiene sia il centro della sfera che l’asse del cilindro (il piano di simmetria trasversale della quartica). Detto piano seziona sia il cilindro sia la sfera secondo, rispettivamente, le generatrici m, n e la circonferenza D; i punti comuni alle dette sezioni sono quelli cercati.
Oltre ai sopraddetti punti notevoli della quartica occorrono altri punti generici come M ed N, che appartengono sia alla circonferenza Y, che ha la 2° P.O. in vera forma, sia alle generatrici m, n; la determinazione di tali sezioni avviene assumendo il piano ausiliario frontale g.
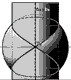 in cui il cilindro ha la sola generatrice b tangente la sfera e le altre
generatrici secanti la stessa. Il risultato dell'intersezione tra le due superfici è una quartica composta da due rami che hanno il punto D in comune, detta finestra di Viviani.
in cui il cilindro ha la sola generatrice b tangente la sfera e le altre
generatrici secanti la stessa. Il risultato dell'intersezione tra le due superfici è una quartica composta da due rami che hanno il punto D in comune, detta finestra di Viviani.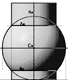 si ha quando il cilindro ha il diametro più piccolo rispetto a quello della sfera ed ha l’asse a passante per il centro c della stessa (fig.9). Il
risultato dell'intersezione è composto da due circonferenze D e F, che oltre ad avere lo stesso diametro del cilindro sono anche
simmetriche rispetto al piano a, poiché passa per il centro della sfera ed ha la giacitura
perpendicolare all'asse del cilindro.
si ha quando il cilindro ha il diametro più piccolo rispetto a quello della sfera ed ha l’asse a passante per il centro c della stessa (fig.9). Il
risultato dell'intersezione è composto da due circonferenze D e F, che oltre ad avere lo stesso diametro del cilindro sono anche
simmetriche rispetto al piano a, poiché passa per il centro della sfera ed ha la giacitura
perpendicolare all'asse del cilindro.Nota: se il diametro del cilindro fosse uguale a quello della sfera non si ha intersezione ma tangenza secondo il parallelo equatoriale
Conclusione: In tutti i casi d'intersezione tra cilindro e sfera, la curva d'intersezione, sia una circonferenza sia una quartica (monogrammica, digrammica), ammette due piani di simmetria: uno con la giacitura contenente gli assi delle due superfici, e l’altro contenente il centro della sfera e perpendicolare all'asse del cilindro.
Intersezione di un cilindro ed una ellissoide (fig.9) 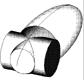
Si pone il caso in cui la curva d’intersezione tra le due superfici, sia composta, da due ellissi, D, G : sezioni della superficie cilindrica con i due piani verticali d, f.
Per la definizione di una superficie di rotazione, secondo il sopracitato principio, occorrono un’asse di rotazione e una curva meridiana. Nel caso in esame l’ellissoide ha b come asse di rotazione (la retta d’intersezione tra i due piani a, b) e H come curva meridiana la cui determinazione avviene ribaltando i vari punti di una delle due ellisse D, G, sul piano frontale b( contenente l’asse b).
La cerniera di ribaltamento è la retta d’intersezione tra i due piani d, f, ad esempio il ribaltamento del punto D^ appartenente all’ellisse G avviene tramite la circonferenze L, che ha come raggio il segmento EˉD^ con direzione perpendicolare all’asse b e come centro il punto E.
Il completamento della detta curva meridiana H (semi ellisse) avviene adottando il
principio della proiettività tra fasci di rette secondo il quale la conica è individuata se sono noti cinque suoi punti.