|
la tecnica qui illustrata ha lo scopo di spiegare in modo
generico di come si può sviluppare una quartica d'intersezione tra due
coni circolari retti, rivolta principalmente a persone hanno una buona
conoscenza dei metodi di rappresentazione della geometria descrittiva. la quartica d'intersezione tra le due superfici coniche è stata trovata utilizzando dei piano ausiliari passanti per i vertici dei due coni. I punti d'intersezione tra le varie generatrici complanari dei ciascun piano ausiliari sono quelli della quartica cercati. in questo caso il tipo di quartica (Q), è digrammica, cioè composta da due rami, che possiamo simbologiare in questo caso, Qi quello inferiore e Qs quello superiore.
|
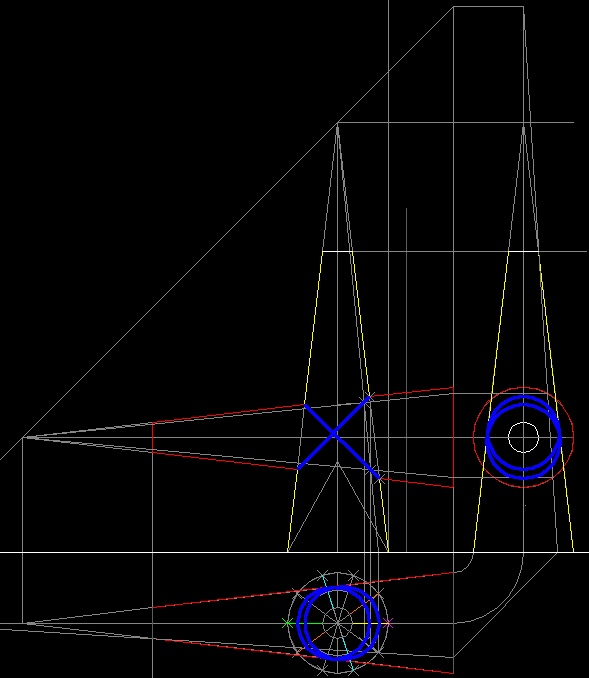 |
| Proiezioni ortogonali "metodo di monge" | |
|
Procedura per lo sviluppo dei due rami delle quartica Qi, Qs
- divedere la circonferenza (dirittrice del cono verticale) in parti uguali, per esempio 10 - consideriamo che il perimetro della circonfenza = H - disegnare un arco di circonferenza A con raggio uguale alla generatrice del cono ed ha il perimetro uguale ad H. - dividere l'arco A in 10 parti (lo stesso numero di parti utlizzato in precedenza) e vi si uniscono con il vertice del cono calcolare le lunghezze dei segmenti di ciascuno dei 11 generatrici, sia quelli riferiti alla parte superiore della quartica Qs , sia quelli della patre inferiore Qi. Per calcolare le generatrici si effetuano i vari ribaltamenti in prima proiezione di ciscun piano verticale conteneti gli stessi generatrici.
|
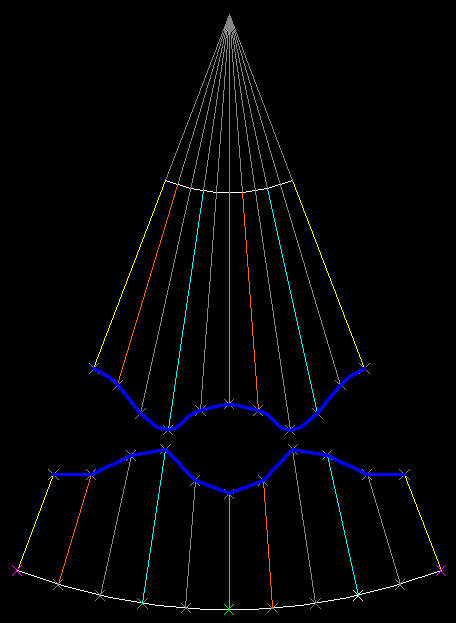 |
| sviluppo della quartica è riferito alla superfice del cono ad asse verticale | |
 |
|
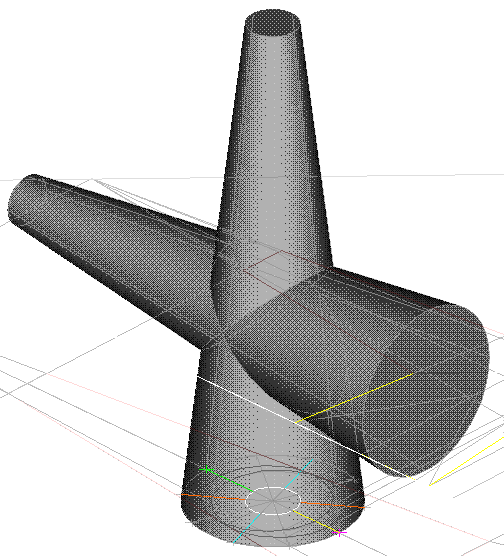
| vista assonometrica |