Al_isawi HomePage / Geometria
/ Costruzione
|
Due figure si definiscono omologhe nei seguenti casi:
- se sono ottenute come proiezioni eseguite da due centri
distinti, della stessa figure sul stesso piano. per esempio sezionare con un
piano Beta due piramidi aventi solo la base in comune. in questo caso la
base è la figura oggettiva da proiettare e le 2 sezioni appartenenti al
piano Beta sono due figure omologhe.
- se sono ottenute come proiezione da un centro di una
stessa figure su due piani distinti. per esempio una piramide sezionata da
due piani distinti (vedi figure)
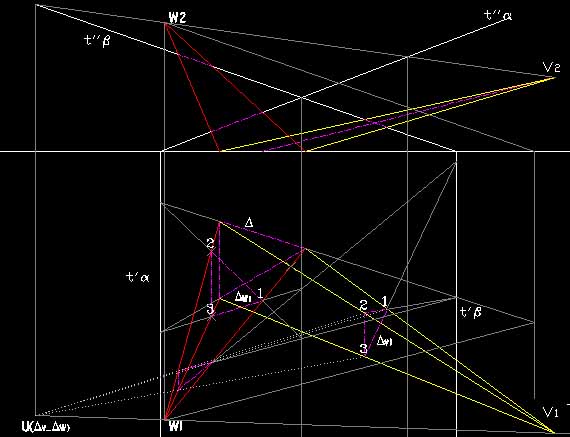
invece non esiste corrispondenza omologica tra due figure
che sono proiezioni eseguite da due centri distinti su due piani distinti.
per esempio due piramidi, aventi solo la base in comune,
sezionati da due piani distinti Alfa e Beta. le due figure che non amettono
corrispondenza, sono le sezioni DeltaV1 ed DeltaW1 |
Tipi di Omologie
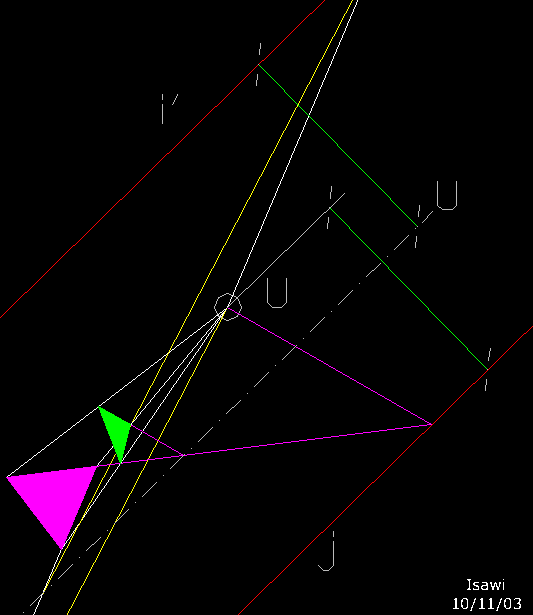 |
|
la figura illustra un caso di omologia dove l'asse u è
in posizione intermedia rispetto alle due rette limiti. |
Alessia scrive:
L'omologia piana si determina quando abbiamo in proiezione un centro, l'asse e: o una coppia di punti corrispondenti, oppure una coppia di
rette corrispondenti, o una delle due rette limite. Le rette limite se rappresentate in una sezione in scorcio totale
hanno ambedue la stessa distanza dal centro c di proiezione e dall'asse, ed è proprio
per questa regola che è possibile disegnare in proiezione una figura conoscendo una delle due rette
limite. Questo implica che le rette limite siano sempre o all'interno o all'esterno della zona delimitata dal centro e dall'asse. Ebbene ho
trovato un disegno su un testo in cui nella proiezione di un cerchio l'asse è tra le due rette limite e il centro è esterno (in basso a
sinistra).Per quale motivo? Questo contravviene alle regole dell'omologia!
Distinti saluti e ringraziamenti per una risposta il più possibile
chiara ed esauriente
Alessia
Isawi risponde:
ciao alessia
Si parla di omologia quando si sceglie un centro S' e si proietta una
figura A su un piano alpha e si ha A' poi si sceglie una altro centro S* e
si proietta la stessa figura A sullo stesso piano e si ha A*, le due figure
proiettate A' -A* hanno tra loro una corrispondenza biunivoca senza eccezioni
dove i punti corrispondenti di A', A* sono allineati con il centro
dell'omologia U e le
rette corrispondenti si incontrano sull'asse dell'omologia u
l'asse dell'omologia è la retta d'intersezione tra il piano oggettivo e
quello di proiezione
il centro dell'omologia è la punto d'intersezione con il piano dell'omologia
della la retta passante per i due centri di proiezioni S',S*
Tipi di Omologia
- omologia speciale: quando le retta passante per i centri di proiezione e
quella passante per i punti corrispondenti si incontrano sull'asse u
- Affinità: quando la retta passante per i due centri di proiezione è
parallela alla retta passante per i due punti corrispondenti, l'omologia in
questo caso può avere diversi aspetti in funzione della direzione del centro
rispetto all'asse dell'omologia:
____- se la direzione è generica rispetto all'asse, si ha l'affinità
obliqua
____- se la direzione è ortogonale rispetto all'asse, si ha l'affinità
ortogonale
Nota: per approfondire il tema dell'affinità clicca qua X
- Omotetia quando si ha come centro un punto proprio (intersezione tra la retta
passante per i due centri di proiezione (proprio, Improprio) con quella passante
per i punti corrispondenti) e come asse dell'omologia una retta impropria (intersezione
tra il piano oggettivo con il piano di proiezione)
- Traslazione: quando centro ed asse dell'omologia sono entrambi impropri
|
Un
esempio di omologica tra la base di un cono quadrico e la vera forma di
una sua sezione generica
|
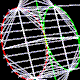 |
| In cui la base appartiene
al primo piano di proiezione (Pigreco 1) e la sezione è stata ottenuta
sezionando il cono con un piano genericamente inclinato (Alpha)
Gli elementi fondamentali dell'omologia
- il centro dell'omologia U, è stato determinato
come punto d'intersezione tra rette passanti per una coppia di punti
corrispondenti assegnata
- l'asse dell'omologia u, è stato stabilito che sia
una retta tangente l'ellisse di base (Delta)
|
|
cono quadrico generico
Dati le proiezioni ortogonali di un cono
quadrico K ( Vedi figura). Si vuole determinare asse principale e
sezione retta di tale cono.
Descrizione degli elementi dati: - un ellisse Delta
appartenente al primo piano di proiezione che funge da base del cono
K.
- un punto V come vertice di K, disposto in modo tale da non
appartenenre ad un piano di simmetria dell'ellisse Delta.
Un passo importante per risolvere tale problema
è quello di determinare uno dei due piani di simmetria di tale cono
per poter risolvere il sopradetto problema, ho cominciato ad
analizzare casi di solidi più semplici come quelli dell'angoloidi (
vedi LINK)
|
Dati |
|
data creazione 29-08-2006
Pagina iniziale
