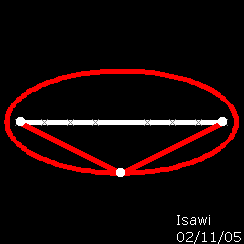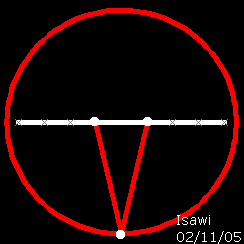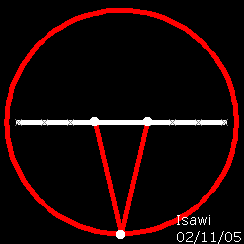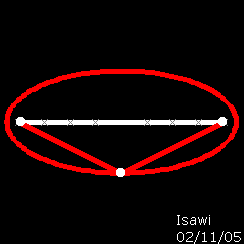
stabilito di avere un ellisse Delta con fuochi F1 ed F2 e deciso di trasformare, con un movimeto nel piano, Delta in un cerchio Delta'

A tale fine ho deciso di allungare l'asse minore dell'ellisse delta fino ad uguagliarlo a quello maggiore di Delta.

A trasformazione completa si può notare che il fuochi F1 ed F2 dell'ellisse delta, sono coincidenti con il centro della circonferenza delta'.

Osservazione

Poiché la circonferenza si considera un caso particolare d'ellisse, non sarebbe  più oppurtuno chiamare i fuochi di un ellisse " centro biforcato dell'ellisse

l'ellisse fa parte di una famiglia di curve piana che sono dette " le coniche", si possono ottenere come sezioni  piane di un cono quadrico. Il termine cono quadrico Include coni come quello di rotazione, ellittic e  iperbolico. Per esempio il cono ellittico viene generato dal movimento ellittico* di una retta a intorno ad una seconda retta a, in cui g ed a sono tra loro complanari. 

*movimento ellittico di una retta g intorno ad una altra retta a ad essa complanare, significa che gli infiniti punti di g descrivono, durante tale movimento, altrettante ellissi omotetiche tra loro.

che è complanare a di rotazione viene generato da una retta g che si muove in modo ciclico intorno ad una altra retta a che è complanare ad g.

lungo una circonferenza che appartiene ad un piano ortogonale  ha come sezione retta un circonferenza, un cono ellittico utilizzato quando si ha almeno una conica come risultato di una sua sezione piana. Le coniche possono essere generate, ciascuno, dal movimento ciclico e vincolato di un punto P rispetto ad uno o più punti. Per esempio un ellisse Delta viene generata dal movimento di P rispetto a due punti fissi F1 e F2 che sono detti i fuochi di Delta.

Curva piana: luogo dei punti che apprtengono ad un medesimo piano.

Curva sghemba: luogo geometrico dei punti che non appartengono ad un stesso piana

Argomenti correlati da sviluppare

Movimento ciclico di un punto nello spazio; distanza di un punto da una conica; distanza di un punto da una quadrica; Curvatura costante; normali ad una curva, Coniche come sezioni di un cono quadrico; prodotto di due o più trasformazione geometrica tra coniche sghembe (come l'elicoidi cilindriche e quelle concoidiche