CAP.   9  -   CIRCONFERENZE E CERCHI 

Definizione:  si chiama circonferenza il luogo dei punti del piano che sono tutti alla stessa distanza da un fisso chiamato CENTRO  della CIRCONFERENZA.     La distanza fissa citata si chiama RAGGIO della CIRCONFERENZA.    La parte interna alla circonferenza si chiama CERCHIO.

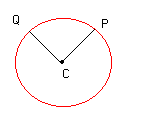        Con riferimento alla figura disegnata si chiama CIRCONFERENZA la parte rossa del disegno, e centro il punto C.    Per definizione presi due punti P,Q sulla circonferenza, deve essere PC= PQ.        Questa distanza fissa viene di solito indicata con r  ( iniziale di raggio).

CORDE  ED  ARCHI    -    DEFINIZIONI

CORDA:    Si indica con tale nome qualunque segmento che unisca due punti situati sulla circonferenza.
ARCO:    Ognuna delle due parti di circonferenza  determinate  da una corda (una ‘sopra’ ed una ‘sotto’).
DIAMETRO:    Quella corda speciale che passa per il centro della circonferenza. 

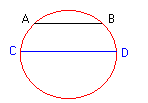
Nel disegno  AB è una corda, mentre CD è una corda che è anche un  DIAMETRO. 
Come semplice proprietà  delle corde e degli archi richiamiamo le seguenti:
Proprietà 1:    Corde di lunghezza uguale sottendono archi di lunghezza uguale.
Proprietà 2:    Corde di lunghezza uguale hanno la stessa distanza dal centro della circonferenza.
Proprietà 3:    La perpendicolare condotta per il punto medio di una corda (quindi più precisamente IL SUO ASSE) passa sempre per il centro della circonferenza stessa. 
Come conseguenza di questa proprietà si ha che il punto di incontro degli assi di due corde E’ IL CENTRO DELLA CIRCONFERENZA.

TANGENTI  E SECANTI 

Occorre ora introdurre altre definizioni relative alla circonferenza prima di passare ad alcuni notevoli teoremi relativi alle proprietà delle circonferenze.

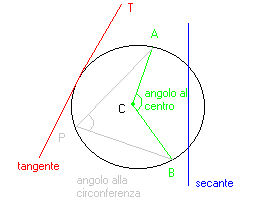
Con riferimento al disegno diamo le seguenti definizioni: 

ANGOLO AL CENTRO     Si intende con tale nome qualunque angolo che parte dal centro C della circonferenza e arriva su due punti situati sulla circonferenza ( A,B ). 

ANGOLO ALLA CIRCONFERENZA    Si intende con tale nome qualunque angolo che parte da un punto P a piacere  situato SULLA  circonferenza e arriva su due punti situati sulla circonferenza. 

TANGENTE ALLA CIRCONFERENZA    Si intende con tale nome qualunque retta che tocca la circonferenza in UN SOLO PUNTO  T. 

SECANTE ALLA CIRCONFERENZA    Si intende con tale nome qualunque retta che tocca la circonferenza in DUE PUNTI.

 PROPRIETÀ DI CORDE  E SECANTI 
Passiamo ora ai seguenti notevoli teoremi sulla circonferenza. 

TEOREMA 1

Fissato un arco di estremi AB, tutti gli angoli alla circonferenza che hanno A,B come punti estremi sono uguali.

TEOREMA 2

Fissato un arco di estremi AB, l’angolo al centro è sempre il doppio dell’angolo alla circonferenza.

TEOREMA 3

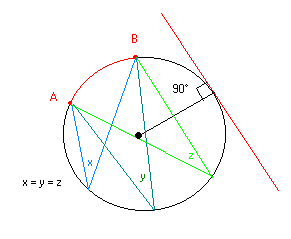
Qualunque retta tangente alla circonferenza in un suo punto T forma una angolo di 90° con il raggio CT che parte dal centro e arriva nel punto di tangenza.

TEOREMA 4   Con riferimento alle figura 1  vale la relazione  AP.PC = BP.PD

Con riferimento alle figura 2  vale la relazione  AP.PC = BP.PD

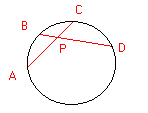
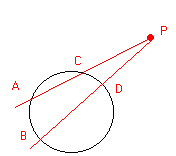
             FIGURA  1                                                                FIGURA  2

A parole:    Date due corde che si intersecano in un punto P il prodotto dei due segmenti in cui ciascuna viene divisa rimane costante (fig. 1).    Condotte due secanti da un punto esterno ad una circonferenza il prodotto tra la secante intera e la sua parte esterna rimane costante.

TEOREMA 5 

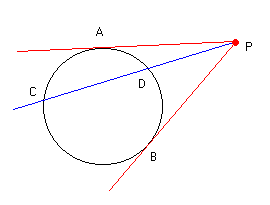
Nella figura che segue vale la relazione:    PB.PC = PA2    a parole: Condotte da un punto esterno ad una circonferenza una secante ed una tangente il prodotto tra l’intera secante e la sua parte esterna è uguale al quadrato della tangente. 

NB: questo teorema  dice anche che fissati il punto P e la circonferenza è possibile  far variare la secante PB  mantenendo però fisso il valore del prodotto PB.PC  ovunque si prenda il punto B sulla circonferenza. Tale prodotto vale sempre PA2.    Otteniamo quindi come conseguenza la seconda delle relazioni del precedente TEOREMA 4.    Poiché inoltre possiamo condurre dal punto P due tangenti, otteniamo anche il risultato che le due tangenti sono uguali. 

PA = PB  e in particolare :        PA2 = PB2 = PC.PD     ovunque venga preso C sulla circonferenza.   

LUNGHEZZA DI UN ARCO

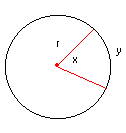
Diamo ora la soluzione del seguente problema: determinare la lunghezza di un arco di circonferenza di raggio r, essendo nota la misura dell’angolo al centro che lo determina.     Nella figura : noto l’arco x e conoscendo r  calcolare la lunghezza y dell’arco.        Sappiamo già dalle scuole medie che la lunghezza della circonferenza intera vale:        2pr e che tutto l’angolo giro vale 360°.

Una semplicissima proporzione ci dice allora che:

         Da cui segue subito la formula voluta per ottenere y:

Anche se per ora non approfondiamo l’argomento lo studente tenga presente che il fattore      ha un ruolo molto importante in matematica poiché serve ad introdurre un nuovo modo di misurare gli angoli.

AREA DI UN SETTORE CIRCOLARE 

Si definisce settore circolare la parte di cerchio compresa tra due raggi.

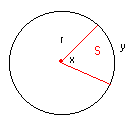        Nella figura il settore circolare è indicato con la lettera S.    Con x abbiamo indicato l’angolo al centro che determina l’arco y.    Sappiamo già che l’area di tutto il cerchio è data da:  pr2.    Ancora una volta una semplice proporzione ci dice che: 

            Da questa formula segue immediatamente che: 

Quindi l’area vale : la lunghezza dell’arco per il raggio diviso 2.   

Va notata la somiglianza di questa formula con quella relativa all’area di un triangolo generico che è data da :  (base per altezza diviso 2 ).        Infine, tenendo conto del valore della y ottenuto prima possiamo anche scrivere: 

           Quindi l’area vale il numero fisso:  per la misura dell’angolo x per il quadrato del raggio. 

Delle formule esposte negli ultimi due paragrafi sono di grande interesse anche le formule inverse, per dedurre raggio r oppure angolo x una volta note le altre grandezze che ricorrono nelle formule.

Lo studente ormai deve sapere che ogni per formula  data si possono dedurre tutte le formule inverse associate e che pure queste sono molto importanti. Ribadiamo  però il concetto fondamentale secondo cui  SOLO UNA FORMULA deve essere ricordata a memoria mentre tutte le inverse che da questa seguono bisogna essere in grado di dedurle per via algebrica, ciò allo scopo di non dover affrontare lo sforzo inutile e stupido  di imparare un numero enorme di formule.

Come ultimo esempio mostriamo come dedurre l’angolo al centro x di una circonferenza di raggio r su cui abbiamo staccato un arco di lunghezza y nota.

La formula di base ( unica da sapere ) dice che: 

   Da cui segue con semplici passaggi:     

Lo studente deve essere allora abbastanza abile nella manipolazione algebrica dei simboli letterali e questo gli può derivare soltanto da uno studio INIZIALE ben fatto delle regole ( in vero ben poche ) ALGEBRICHE, CHE QUINDI RIBADIAMO COME FONDAMENTALI PER LE APPLICAZIONI PRATICHE IN GEOMETRIA E NATURALMENTE ANCHE IN TUTTE LE SCIENZE APPLICATE.

Torna all'indice