|
lo studio sui angoloidi
nasce in origine dal seguente requisito
|
|
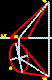
Dati le proiezioni ortogonali di un cono
quadrico K ( Vedi figura). Si vuole determinare asse principale e
sezione retta di tale cono.
Descrizione degli elementi dati: - un ellisse Delta
appartenente al primo piano di proiezione che funge da base del cono
K.
- un punto V come vertice di K, disposto in modo tale da non appartenere
ad un piano di simmetria dell'ellisse Delta
Un passo importante per risolvere tale problema
è quello di determinare uno dei due piani di simmetria di tale cono |
Dati |
| |
|
Sezione retta di un tetraedro simmetrico
Determinare la sezione retta di una
dato tetraedro simmetrico K. La soluzione
consiste nel determinare, in ordine, l'asse
di K, come retta d'intersezione tra il piano di simmetria alpha con il piano
bisettore le facce incidenti alpha, e quella di sezionare K con un piano
avente giacitura perpendicolare all'asse di K.
|
 |
|
|
|
|
Due date rette sghembe individuano un solo poliedro tetraedrico
unire i soli estremi di due segmenti A_B, C-D
appartenenti a rette sghembe, nel insieme ed in ogni caso, individua nello
spazio gli spigoli di un poliedro triedrico.
Nella forma più laboriosa, la trasformazione biunivoca di
numerosi punti di tali segmenti, genera la classica superficie rigata
|
 |
|
|
|
|
|
|
|
Dati le P.O. di un angoloide tetraedrico K avente come
sezione un trapezio scaleno, si vuole determinare uno dei due biconi
inviluppato da tale angoloide K.
|
 |
 |
|
Dato un angoloide tetraedrico K avente come sezione un trapezio scaleno. si
vuole determinare il cono quadrico da esso inviluppato
in questo caso è stato possibile determinare un parallelogramma R come
sezione di tale angoloide K e anche un ellisse Delta
inscritta da R. Purtroppo, non è stato
possibile individuare gli elementi principali ( asse e sezione normale) del
cono cercato, quello che dovrebbe avere come propria sezione tale ellisse
Delta.
|
 |
|
Per poter costruire un angoloide tetraedrico quadrico* ,
bisogna determinarvi un eventuale suo piano di simmetria.
* angoloide quadrico, quello che ammette che le proprie
facce siano tangenti una quadrica
|
 |

|
|
11/10/05-
Dati le proiezioni ortogonali di un tetraedro generico. Determinare il cono
quadrico che inviluppa tale tetraedro.
Nota: per modellare il cono inviluppatore il tetraedro, è
indispensabile la determinazione del suo asse principale.
|
 |
|
|
|
|
Bisettrici di un angoloide
|
|
|
BisettroideF: la retta che ha la proprietà di essere il
luogo geometrico dei punti equidistanti dalle facce di un angoloide
triedro. Perciò si può
concludere dicendo che tutti gli angoloidi triedri possono
essere iinviluppatori di coni di rotazione.
|
 |
|
BisettroideS: la retta che ha la proprietà di essere il
luogo geometrico dei punti equidistanti dagli spigoli di un angoloide
triedro.
Perciò si può concludere
dicendo che tutti gli angoloidi triedri possono essere inviluppati da
coni di rotazione. inoltre questa conclusione può essere estesa a tutti gli
angoloidi poliedrici che ammettono, ciascuno, come propria sezione, un
poligono che può essere inscritto in una circonferenza?
|
 |
|
|
|
|
angoloide triedro
osservazione
sezionando il triedro con piano
generico alpha, si ha logicamente un triangolo circoscritto (vedi figure) da una circonferenza Delta.
Il quale può essere la sezione
di infinite sfere che hanno tutte i centri sulla retta passante per il
centro di delta e direzionata perpendicolarmente al piano alpha.
|
 |
|
Analogo ragionamento, vedi sopra, si può fare con la circonferenza
inscritta in una sezione generica di un triedro
|
 |
|
|
|
|
la bisettrice di un angoloide triedro, si determina
come retta comune ai piani bisettore le facce di tale angoloide.Un triedro K
ammette in tutti i casi che le proprie facce sia tangenti ad una sfera delta
che ha centro sulla bisettrice di K, e ne consegue che il cono Gamma che ha
...
|
 |
 |
|
|
|
Tetraedro e coni quadrici
dato un tetraedro K con base equilatera inscrittibile e
circoscrittibile da due coniche chiuse. si ha che tale tetraedro
sarà sicuramente inviluppante ed inviluppato da due coni quadrici
che possono essere sia di rotazione sia ellittici.
l'asse del cono inviluppato da K viene determinato come
retta comune ai piani che bisecano, due a due, le facce opposte di K.
l'asse del cono inviluppante il tetraedro K viene
individuato da una retta che
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|